Podstawy grafiki 3D

---

1. Ściana
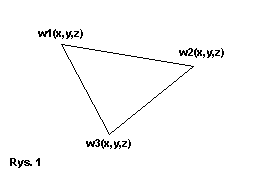
Ściana jest wielokątem, który składa się z minimum trzech wierzchołków, z których każdy posiada współrzędne x, y, z. Ściana składająca się z trzech wierzchołków została pokazana na Rys. 1:

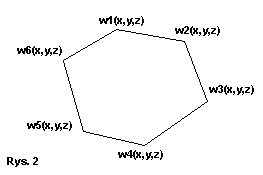
Ściana składająca się z sześciu wierzchołków została pokazana na Rys. 2:

2. Przechowywanie danych ściany
Jedną z metod przechowywania danych ściany są tablice wierzchołków i indeksów. Indeksy różnych ścian w tablicy indeksów mogą wskazywać na te same wierzchołki, co umożliwia kompresję informacji o wierzchołkach. Dla ściany składającej się z trzech wierzchołków wygląd tablic wierzchołków i indeksów jest pokazany poniżej.


3. Wektor
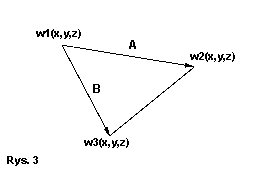
Wektor jest odcinkiem skierowanym którego współrzędne wyznaczamy następująco:
Wektor A = [ w2.x - w1.x, w2.y - w1.y, w2.z - w1.z ]
Wektor B = [ w3.x - w1.x, w3.y - w1.y, w3.z - w1.z ]

4. Długość wektora
Wyznaczamy ją ze wzoru:
Długość wektora A = || A || = sqrt ( A.x*A.x + A.y*A.y + A.z*A.z )
gdzie sqrt to pierwiastek kwadratowy

5. Normalizacja
Polega na sprowadzeniu długości wektora do jedności.
Normalizujemy dzieląc składowe wektora przez jego długość.
Wektor znormalizowany A = A / || A || = [ A.x / ||A||, A.y / || A ||, A.z / || A || ]
Normalizacja najczęściej zapisywana jest w postaci funkcji o nazwie Normalize.
Noramlize( A ) to normalizacja wektora A.
Biblioteki OpenGL i DirectX mają zaimplementowaną funkcję Normalize.

6. Iloczyn skalarny
Iloczyn skalarny dwóch wektorów A i B jest liczbą wyznaczoną ze wzoru:
Iloczyn skalarny wektorów A i B = A o B = A.x*B.x + A.y*B.y + A.z*B.z
Iloczyn skalarny wektorów A i B = A o B = || A || * || B || * cos( A, B )
Gdy A i B są znormalizowane to A o B = cos(A,B), czyli iloczyn skalarny jest równy cosinusowi kąta pomiędzy wektorami A i B.
Iloczyn skalarny najczęściej zapisywany jest w postaci funkcji o nazwie DotProduct.
A o B = DotProduct( A, B )
Biblioteki OpenGL i DirectX mają zaimplementowaną funkcję DotProduct.

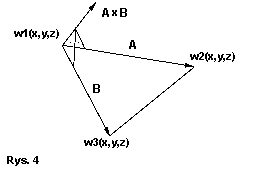
7. Iloczyn wektorowy
Iloczyn wektorowy dwóch wektorów A i B jest wektorem prostopadłym do A i B wyznaczonym ze wzoru:
Iloczyn wektorowy A i B = A x B = [ A.y*B.z - B.y*A.z, B.x*A.z - A.x*B.z, A.x*B.y - B.x*A.y ]

Iloczyn wektorowy najczęściej zapisywany jest w postaci funkcji o nazwie CrossProduct
A x B = CrossProduct( A, B )
Biblioteki OpenGL i DirectX mają zaimplementowaną funkcję CrossProduct.

8. Wektor normalny
Jest wektorem prostopadłym do płaszczyzny i jest wyznaczany z iloczynu wektorowego. Długość wektora normalnego wynosi jeden ponieważ jest on wektorem znormalizowanym.
A x B = CrossProduct( A, B )
Wektor normalny N = Normalize( A x B )

9. Płaszczyzna
Jest określona przez równanie płaszczyzny wzorem:


P to dowolny wierzchołek leżący na płaszczyźnie.
N to wektor normalny płaszczyzny wyznaczony np. z wierzchołków ściany leżącej na tej płaszczyźnie.
D to przesunięcie płaszczyzny.
Płaszczyznę przechowujemy w postaci wektora normalnego N i przesunięcia D

10. Płaszczyzna prostopadła do krawędzi ściany
Musimy znać wektor R wyznaczony z wierzchołków krawędzi ściany oraz wektor normalny N ściany.
Wtedy:


Gdzie:
SD, SN to odpowiednio przesunięcie oraz wektor normalny szukanej płaszczyzny prostopadłej do krawędzi ściany.
P to jeden z wierzchołków krawędzi ściany np. pierwszy.

11. Duży portal (ang. Huge portal)
Jest ścianą zbudowaną na powierzchni płaszczyzny. Poniżej opisany jest algorytm pozwalający wyznaczyć cztery wierzchołki dużego portala. Jest to algorytm tworzenia ściany na płaszczyźnie. Płaszczyzna jest określona przez wektor normalny N i przesunięcie D.


Wartość 20000 została przyjęta orientacyjnie. Wielkość dużego portala powinna być ustalana w taki sposób, aby jego wymiary były dużo większe od wymiarów sceny lub dopasowane do wielkości sześcianu ograniczającego scenę.


Dla każdego z czterech wierzchołków dużego portala wyznaczamy jego składowe x, y, z:
duży portal[ numer wierzchołka ].x = W1.x * wymiary portala[ numer wierzchołka ].x + W2.x * wymiary portala[ numer wierzchołka ].y + WD.x
duży portal[ numer wierzchołka ].y = W1.y * wymiary portala[ numer wierzchołka ].x + W2.y * wymiary portala[ numer wierzchołka ].y + WD.y
duży portal[ numer wierzchołka ].z = W1.z * wymiary portala[ numer wierzchołka ].x + W2.z * wymiary portala[ numer wierzchołka ].y + WD.z
Numer wierzchołka wynosi 1, 2, 3, 4.

12. Sprawdzenie położenia punktu P względem płaszczyzny
Płaszczyzna określona jest poprzez:
Wektor normalny płaszczyzny N = [ N.x, N.y, N.z ].
Przesunięcie płaszczyzny D.

Położenie punktu P względem płaszczyzny sprawdzamy rozwiązując równanie płaszczyzny DotProduct( N, P ) + D dla współrzędnych punktu P i testując znak wyniku. Gdy wynik jest równy zero to punkt leży na płaszczyźnie. Gdy wynik jest dodatni bądź ujemny to punkt leży po jednej ze stron płaszczyzny. Wynik wyrażenia DotProduct( N, P ) + D jest rozwiązaniem równania płaszczyzny dla współrzędnych punktu P.

13. Sprawdzenie położenia ściany względem płaszczyzny
Polega na sprawdzeniu położenia jej wierzchołków względem płaszczyzny. Gdy wszystkie wierzchołki leżą na płaszczyźnie to ściana leży na płaszczyźnie. Gdy wszystkie wierzchołki leżą po jednej ze stron płaszczyzny to ściana leży po jednej ze stron płaszczyzny. Gdy część wierzchołków leży po jednej ze stron płaszczyzny to płaszczyzna przecina ścianę.

14. Sprawdzenie zwrotu ściany
Zwrot ściany w przestrzeni 3D jest ustalany względem wybranego punktu odniesienia, którym może być np. pozycja obserwatora. Sprawdzenie zwrotu ściany polega na rozwiązaniu równania płaszczyzny dla współrzędnych obserwatora i sprawdzeniu znaku wyniku. Jeżeli wartość wynikowa jest dodatnia lub ujemna to ściana jest zwrócona przodem lub tyłem do obserwatora. Jeżeli wartość wynikowa jest równa zero to obserwator leży na płaszczyźnie ściany.

15. Usunięcie ścian niewidocznych (ang. cull face)
Polega na sprawdzeniu zwrotu wszystkich ścian, które chcemy wyświetlić i usunięciu tych, które są ustawione tyłem do obserwatora.

16. Przecięcie odcinka z płaszczyzną
Płaszczyzna jest dana poprzez wektor normalny N i przesunięcie D.
Odcinek jest dany poprzez punkt początkowy PP i końcowy KP.
Wyznaczamy wektor kierunkowy V = PP - KP.
Współrzędnych wektora V nie normalizujemy.


17. Przecięcie odcinka ze ścianą
W metodzie tej rozwiązujemy równanie płaszczyzny ściany dla współrzędnych początkowych i końcowych odcinka, a następnie sprawdzamy znak wyniku. Jeżeli stwierdzimy, że znak wyniku otrzymany dla współrzędnych początkowych jest różny od znaku wyniku otrzymanego dla współrzędnych końcowych, to istnieje możliwość kolizji ze ścianą. Wyznaczamy wtedy punkt przecięcia płaszczyzny ściany z odcinkiem. Następnie sprawdzamy czy punkt przecięcia znajduje się wewnątrz ściany. Jeżeli punkt przecięcia znajduje się wewnątrz ściany to kolizja wystąpiła.

Realizacja:
Obserwator jest w punkcie A(x, y, z) i wykonał ruch do punktu B(x, y, z).
Sprawdzamy czy wystąpiła kolizja ze ścianą o wierzchołkach w1,w2,w3,w4 dla której mamy policzone:

• równanie płaszczyzny zapisane w postaci wektora normalnego N i przesunięcia D (wyznaczamy z punktu 9).
• równania czterech płaszczyzn (p1, p2, p3, p4) prostopadłych do krawędzi ściany zapisanych w postaci N1, D1 N2, D2 N3, D3 N4, D4 (wyznaczamy z punktu 10)

---

Numer artykułu: 2
Wysłany: Sat, Jan 23, 2010 6:47 PM
Ostatnio zmieniony: Sun, Feb 14, 2010 3:16 PM

Adres URL: https://www.komires.net/article.php?id=2